Dimension Reduction Techniques : Introduction

• Dimension reduction is a strategy with the help of which, data from high dimensional space can be converted to low dimensional space. This can be achieved using any one of the two dimension reduction techniques :
  • Linear Discriminant Analysis(LDA)
  • Principal Component Analysis(PCA) 

1. Linear Discriminant Analysis(LDA)

   • Linear discriminant analysis i.e. LDA is one of the dimension reduction techniques which is capable of discriminatory information of the class.
   • The major advantage of using LDA strategy is, it tries to obtain directions along with classes which are best separated.
   • Scatter within class and Scatter between classes, both are considered when LDA is used.
   • Minimizing the variance within each class and maximizing the distance between the means are the main focus of LDA.
   
   

   Algorithm for LDA

   • Let the number of classes be “c” and u_i be the mean vector of class i, where i=1,2,3,.. .
   • Let N_i be the number of samples within class i, where i=1,2,3…C.
   • Total number of samples,  N=∑ Ni.
   • Number of samples within Class Scatter Matrix.
   
   
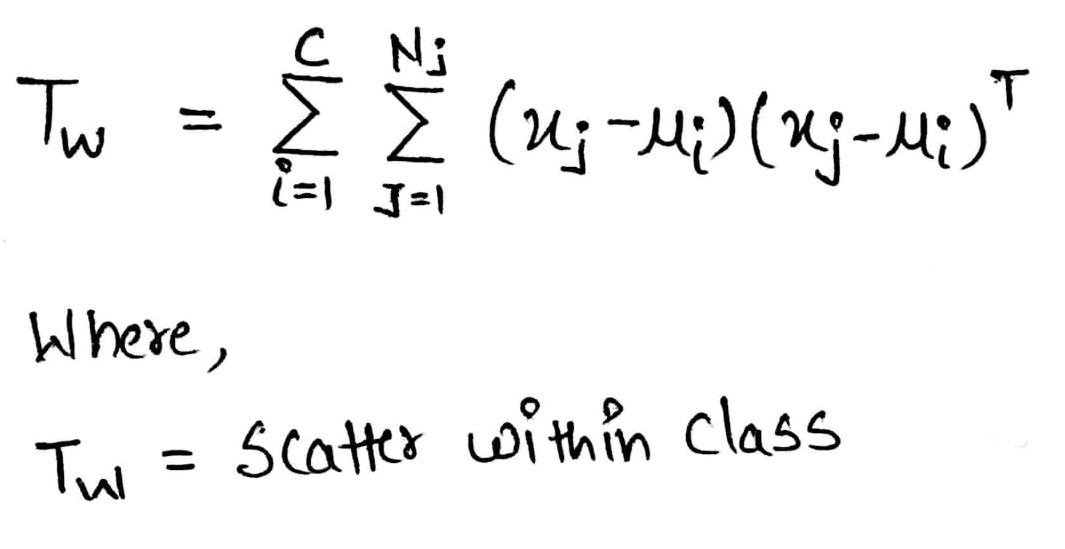
   Scatter Within Class
   
   • Number of samples between Class Scatter Matrix.
   
   
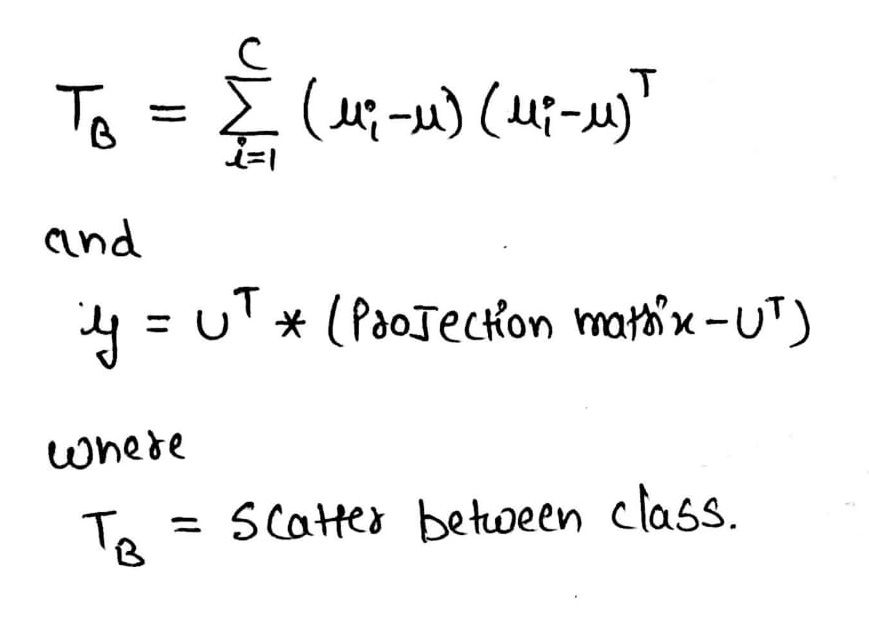
   Scatter Between Class
   

   Advantages : Linear Discriminant Analysis

   • Suitable for larger data set.
   • Calculations of scatter matrix in LDA is much easy as compared to co-variance matrix.

   Disadvantages : Linear Discriminant Analysis

   • More redundancy in data.
   • Memory requirement is high.
   • More Noisy.

   Applications : Linear Discriminant Analysis

   • Face Recognition.
   • Earth Sciences.
   • Speech Classification.
    

2. Principal Component Analysis(PCA)

   • Principal Component Analysis i.e. PCA is the other dimension reduction techniques which is capable of reducing the dimensionality of a given data set along with ability to retain maximum possible variation in the original data set.
   • PCA standouts with the advantage of mapping data from high dimensional space to low dimensional space.
   • Another advantage of PCA is, it is able to locate most accurate data representation in low  dimensional space.
   • In PCA, Maximum variance is the direction in which data is projected.
   
   

   Algorithm For PCA

   • Let d₁,d₂, d₃,…,d_d be the whole data set consisting of d-dimensions.
   • Calculate the mean vector of these d-dimensions.
   • Calculate the covariance matrix of data set.
   • Calculate Eigen values(λ₁,λ_2,λ_3,…,λ_d) and their corresponding Eigen vectors (e₁, e₂, e₃,….e_d).
   • Now, Sort the Eigen vectors in descending order and then choose “p” Eigen vectors having largest values in order to generate a matrix “A” with dimensions p*d.

   i.e. A = d * p.

   • Using the matrix “A” (i.e. A = d * p) in order to transform samples into new subspace with the help of:

   y = A^T * x

   Where, A^T Transpose matrix of “A”

   Advantages : Principal Component Analysis

   • Less redundancy in data.
   • Lesser noise reduction.
   • Efficient for smaller

   Disadvantages : Principal Component Analysis

   • Calculation of exact co-variance matrix is very difficult.
   • Not suitable for larger data sets.

   Applications : Principal Component Analysis

   • Nano-materials.
   • Neuroscience.
   • Biological Systems.