Non-Parameter Estimation : Density Estimation

• Density Estimation is a Non-Parameter Estimation technique which is used to determine the probability density function for a randomly chosen variable among a data set.
• The idea of calculating unknown probability density function can be done by:

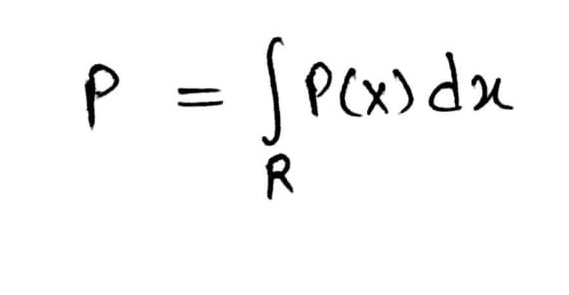
Density Estimation

where,

“x” Denotes sample data i.e. x1, x2, x3,..,xn on region R.

P(X) denotes the estimated density and

P denotes the average estimated density.

• In order to calculate probability density estimation on sample data “x”, it can be achieved by:

Density Estimation

• Histogram is one of the simplest way used for density estimation.
• Other approaches used for non-parametric estimation of density are:
  • Parzen Windows.
  • K-nearest Neighbor.

Non-Parameter Estimation: Parzen Windows

• Parzen windows is considered to be a classification technique used for non-parameter estimation technique.
• Generalized version of k-nearest neighbour classification technique can be called as Parzen windows.
• Parzen Windows algorithm is based upon the concept of support vector machines and is considered to be extremely simple to implement.
• Parzen Windows works on the basis of considering all sample points of given sample data based on scheme of voting and assigning weights w.r.t the kernel function. It does not consider the neighbors and labelled weights.
• Also, it does not requires any training data as it can affect the speed of operation.
• Parzen windows decision function can be represented by:

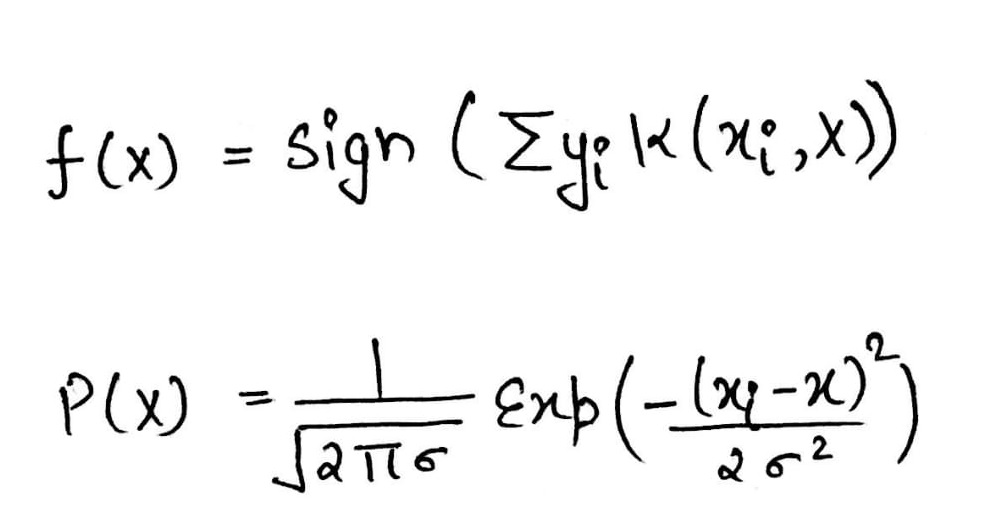
Parzen Window

where, P(X) is the Gaussian function which is also known as Parzen probability density estimation in 2-D.

Non-Parameter Estimation : K-Nearest Neighbor

• K-Nearest Neighbor is another method of non-parameter estimation of classification other than Parzen Windows.
• K-Nearest Neighbor( also known as k-NN) is one of the best supervised statistical learning technique/algorithm for performing non-parametric classification.
• In K-Nearest Neighbor algorithm, class of an object is determined on the basis of class of its neighbor.

How It Works?

• Consider a training sample of Squares and circles and circles. Now we need to classify the “Star” Shape on the basis of its neighbors i.e. Squares and Circles.
• Let x_i be the training sample and “k” be the distance from the position of “Star” shape.

k-NN algorithm

Disadvantages : Using K-NN

• Expensive.
• High Space Complexity.
• High Time Complexity.
• Data Storage Required.
• High-Dimensionality of Data.