SEARCHING STRATEGIES IN AI


Searching Strategies | Artificial Intelligence Tutorial | Minigranth

 Searching Strategies : Introduction

  • Searching is a process to find the solution for a given set of problems. This in artificial intelligence can be done by using either uninformed searching strategies of either informed searching strategies.

Un-Informed Search Strategy

  • Un-Informed search strategy further includes two techniques. These are:
    1. Breadth First Search.
    2. Depth First Search.

Breadth First Search

  • In Breadth First Search(BFS), the root node of the graph is expanded first, then all the successor nodes are expanded and then their successor and so on i.e. the nodes are expanded level wise starting at root level.
  • For Example :
 
This image describes an example of breadth first search. It is one of the two searching strategies that is widely used.
Searching Strategies : Breadth First Search
 

Depth First Search

  • In Depth First Search(DFS), the deepest node is expanded in the current unexplored node of the search tree. The search goes into depth until there is no more successor nodes.
  • For Example :
 
This image describes the other strategy of searching in artificial intelligence known as depth first search.
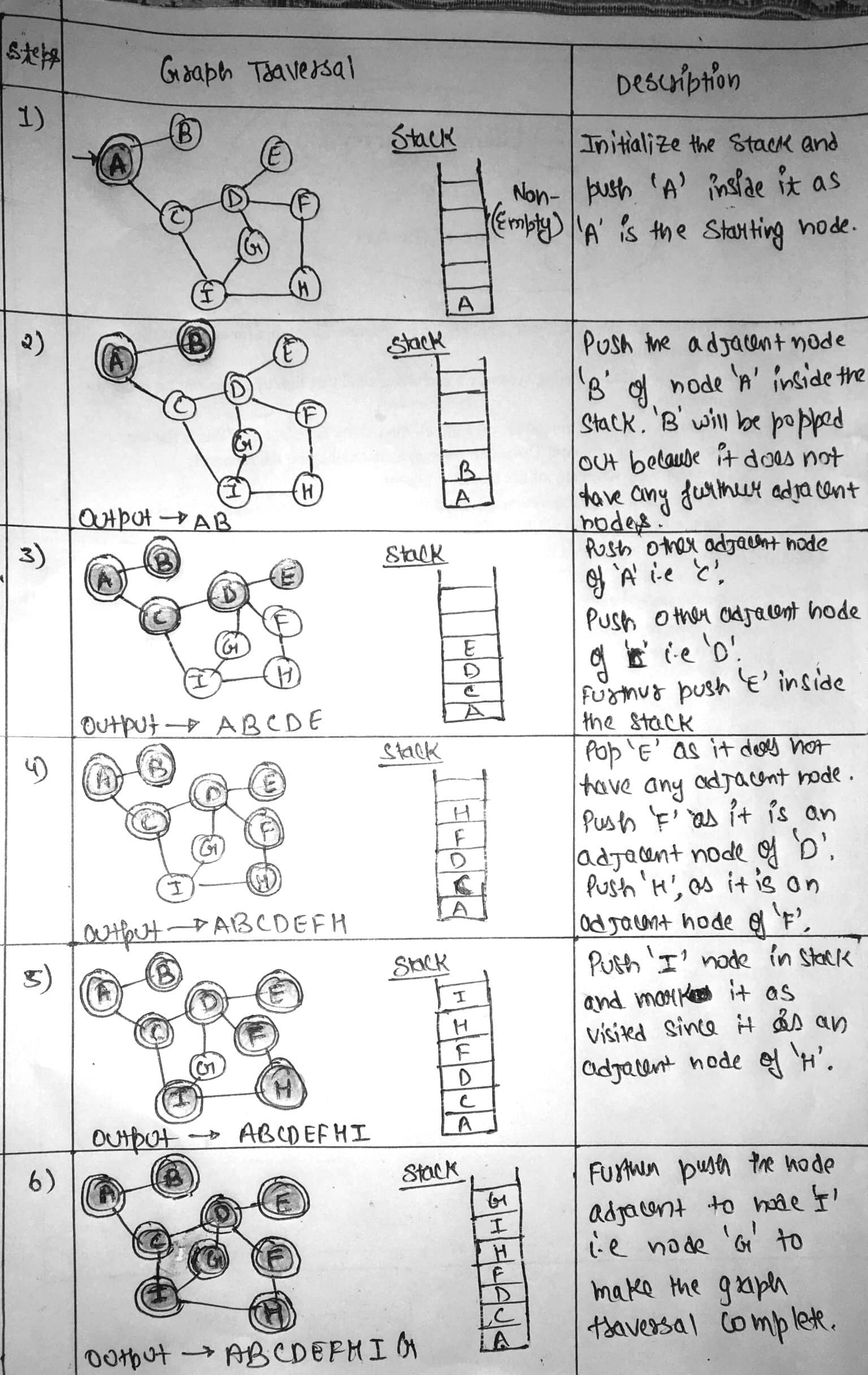
Searching Strategies : Depth First Search
 

Informed Search Strategy

  • Informed search strategy further includes two searching techniques. These are:
    1. A* Search Technique.
    2. AO* Search Technique.
A* Search Technique
  • A* search technique is an informal search strategy but can be called as a form of best first search.
  • It is a search technique which the most optimistic node is expanded by expanding a graph.
  • The node of the graph can be evaluated by using two functions i.e. g(n) and h(n).
Here,
g(n) = Cost/Distance to reach node “n”.
h(n) = Cost/Distance to reach from node “n” to the goal node.
  • For evaluating any node, function f(n) is generated and used as:
f(n) = g(n) + h(n).
where,
f(n) = Estimated cost/distance of solution through node “n”.  

A* Technique : Working
  • In the first step, two sets are maintained:
    1. OPEN SET:: It contains the set of nodes that needs to be visited/Examined.
    2. CLOSED SET:: It contains the set of nodes that have already been visited or examined.
  • Every individual node “n” maintains the function g(n), h(n) and f(n).
  • Each node also maintains link pointer to its parent node s that the best solution can be retrieved, if found.
AO* Algorithm
  • AO* algorithm is the modified version of A* algorithm in order to cover up the limitations of A* algorithm.
  • The AO* uses a single structure i.e. “G”, unlike two sets OPEN and CLOSE that was used in A* algorithm.
  • The structure “G” represents the part of the graph that has been generated so far.
  • Each node of the structure “G” is always connected either to its immediate successor or predecessor.
  • The nodes of the structure “G” also contains their respective distance/cost from each other.
  • The cost between the starting node to current node “n” of structure “G” is not stored.
  • Through this, AO* is always able to find solutions with minimum cost. 

Previous Next